Denary / decimal (base 10)
This is our everyday counting system. Here is an example, the decimal number 5126 ..
| Possible digits 0-9 | 5 | 1 | 2 | 6 |
|---|---|---|---|---|
| Units | 1000's | 100's | 10's | 1's |
| To the power of | 103 | 102 | 101 | 100 |
Before decimalisation in the UK we used base 12 (imperial) derived from the seasons and the phases of the moon.
Binary (base 2)
Base 2 uses only 0’s and 1's. Computers use this. Early computers employed simple switches (electro magnets relays closed and released/opened) to represent 0's and 1's. Then came vacuum tubes followed by transistors. Binary is the obvious counting base for computers.
Early computers had an 8-bit architecture. This means they were able to calculate one 8-digit number at a time. These 8-digit numbers are called Bytes.
Each individual digit of a Bytes is called a Bit.
Here is an example of an 8-bit byte. The number represented is decimal 218 ..
| Possible digits 0 or 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| Units | 128's | 64's | 32's | 16's | 8's | 4's | 2's | 1's |
| To the power of | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
Nibbles
8-bit bytes can be divided into two 4 bit parts called Nibbles . ..
| 1st nibble | 2nd nibble | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
A nibble can represent 16 numbers, from 0 to 15.
| Binary | Decimal |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
| 1100 | 12 |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
Byte values
In binary, the smallest possible number an 8-bit byte can represent = 00000000 (8 zero’s) , or 0 in decimal.
The biggest number an 8-bit byte can represent = 11111111 (8 one’s) or 255 in decimal.
Incidentally, 1024 Bytes = 1 kilobyte (1K). 1024K (roughly a million bytes) = 1 megabyte (1mb).
MSB and LSB
In a binary, the bit furthest to the left is known as the most significant bit (MSB) and the bit furthest to the right is known as the least significant bit (LSB).
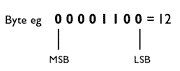
The MSB is used to identify (or sign-post) what kind of byte it is. For example:
In the MIDI language, MIDI messages are comprised of a number of bytes. A single status byte is followed by one or more data bytes.
A byte with an MSB of 1 indicates a status byte. These bytes define what the message is, such as change the sound volume.
A byte with an MSB of 0 indicates a data byte. These bytes carry data values.
For example ..
10011001 01101011
Hexadecimal (base 16)
Hexadecimal makes it possible to represent large binary and decimal numbers with fewer characters. It can work like shorthand. Hexadecimal is often referred to as Hex. When we discuss or write down Hex numbers we put an H after them so we know they are hex. Here are some examples ..
| Decimal | Hexadecimal (hex) equivalent |
|---|---|
| 22 | 16H |
| 81 | 56H |
| 185 | B9H |
| 255 | FFH |
In hex the numbers 0 to 9 are represented with numbers, but above 9 they are represented with letters. So ..
- the symbols "0"–"9" represent values 0 to 9
- the symbols "A"–"F" to represent values from 10 to 15
Here is a partial decimal to 8-bit binary to hex conversion chart ..
| Decimal | Binary | Hexadecimal (hex) |
|---|---|---|
| 0 | 00000000 | 00H |
| 1 | 00000001 | 01H |
| 2 | 00000010 | 02H |
| 3 | 00000011 | 03H |
| 4 | 00000100 | 04H |
| 5 | 00000101 | 05H |
| 6 | 00000110 | 06H |
| 7 | 00000111 | 07H |
| 8 | 00001000 | 08H |
| 9 | 00001001 | 09H |
| 10 | 00001010 | 0AH |
| 11 | 00001011 | 0BH |
| 12 | 00001100 | 0CH |
| 13 | 00001101 | 0DH |
| 14 | 00001110 | 0EH |
| 15 | 00001111 | 0FH |
| 16 | 00010000 | 10H |
| 17 | 00010001 | 11H |
| 18 | 00010010 | 12H |
| 19 | 00010011 | 13H |
| 20 | 00010100 | 14H |
| 51 | 00110011 | 33H |
| 81 | 01010001 | 51H |
| 83 | 01010011 | 53H |
| 112 | 01110000 | 70H |
| 128 | 10000000 | 80H |
| 173 | 10101101 | ADH |
| 185 | 10111001 | 59H |
| 255 | 11111111 | FFH |
This is an example of a hex number ..
| Possible digits 0 to 9 and A to F | F | 3 |
|---|---|---|
| Units | 16's | 1's |
| To the power of | 161 | 00 |
In this example the hex number is (15 (F) x 16) + (3 x 1) which is equal to 243 in decimal, 11110011 in binary, or F3h in hex. You can see that we have converted an 3 or 8 digit number into 2 digits.
Here is another example of a hex number ..
| Possible digits 0 to 9 and A to F | F | F |
|---|---|---|
| Units | 16's | 1's |
| To the power of | 161 | 00 |
In this example the hex number is (15 (F) x 16) + (15 x 1) which equals 255 in decimal, 11111111 in binary, or FFh in hex.
The biggest number hex can express in 2 columns (or bits) is FFH (15 x 16 + 15) = 255 in decimal.
Biggest number in 8 bit binary = 11111111 = 255.
Thus a 1 or 2 bit hex number can represent any 8 bit binary byte.
MIDI (Musical Instrument Digital Interface) & Hexadecimal
8-bit languages are relative primitive by today’s standards, but they are useful to study when trying to understand how binary and hex works.
MIDI is an example of an 8-bit language. It is used by music makers. It allows an interconnected network of electronic musical instruments and computers to be connected together. Find out more here
MIDI users (musicians for example) do not input and edit MIDI data with computers at binary level. When they change MIDI value parameters (such as volume) in applications such as Logic or Cubase, they use decimal. Logic and Cubase can record, edit and replay MIDI.
If you think about it, Logic and Cubase are nothing more than applications designed to record edit, replay and store MIDI events, whilst presenting them to the end user graphically and numerically in a familiar counting base (ie decimal). But under the hood its all binary (1s and 0s). (They also handle audio of course).
Because MIDI is tied to a hardware specification (ports, cables and hardware devices such as keyboards etc) it has remained an 8-bit language. Other software elements in a computer system may be 16, 24, 32 or 64-bit. Click here to read more.
Hex is base 16. Because MIDI is an 8-bit language (nice and simple to understand!) its ideal to study when trying to understand how hex works. In fact MIDI is often displayed in hex to make editing and manipulation of some MIDI commands easier to understand (such as Systems Exclusive).
Between the decimal interface of Logic or Cubase, and the underlying binary computer machine code, MIDI can be manipulated with the more succinct and convenient counting base of hex. To facilitate the control of systems exclusive messages sequencers often have screens/pages where MIDI data is presented in hex form.
Every 8-bit MIDI value can be expressed by a 2 digit hex number. For example; the MIDI byte 10010011 is 147 in decimal or 93H in hex.
